Plane elastostatics with two different isotropic materials

We depart from the minimal example for plane elastostatics. The domain is divided into three horizontal stripes, where the elastic properties of the central stripe differ from the remaining part.

Note

You can download the complete python script heteroPlaneElast.py

Apart from changing the name of the output file, only the section Constitutive Law is affected. Therefore, we discuss in detail only this section.

#---------------------------------------------------------------------
# CONSTITUTIVE LAW
#---------------------------------------------------------------------
# Strain function
def epsilon(u):
    return ufl.sym(ufl.grad(u))

# Stress function
def sigma(u):
    return lmbda*ufl.nabla_div(u)*ufl.Identity(2) + 2*mu*epsilon(u)

E  = YoungMod
nu = PoissonNr

factor_C = 10.0

model = "plane_stress"

mu_c    = E/2/(1+nu)                          # reference Lame constants
lmbda_c = E*nu/(1+nu)/(1-2*nu)

if model == "plane_stress":
    lmbda_c = 2*mu_c*lmbda_c/(lmbda_c+2*mu_c)

mu_0    =  mu_c                               # Lame constants in subdomain 0
lmbda_0 = lmbda_c

mu_1    = factor_C*mu_c                       # Lame constants in subdomain 1
lmbda_1 = factor_C*lmbda_c

def Omega_0(x):    
    listA = [strip_height <= y <= 2*strip_height  for y in x[1]]
    return np.array(listA) 

def Omega_1(x):
    listB = [y >= 2.0*strip_height or y <= strip_height  for y in x[1]]
    return np.array(listB) 

cells_0 = mesh.locate_entities(my_mesh, my_mesh.topology.dim, Omega_0)
cells_1 = mesh.locate_entities(my_mesh, my_mesh.topology.dim, Omega_1)

Q = fem.functionspace(my_mesh, ("DG", 0))

mu    = fem.Function(Q)
lmbda = fem.Function(Q)

mu.x.array[cells_0]    = np.full_like(cells_0, mu_0, dtype=PETSc.ScalarType)
mu.x.array[cells_1]    = np.full_like(cells_1, mu_1, dtype=PETSc.ScalarType)

lmbda.x.array[cells_0]  = np.full_like(cells_0, lmbda_0, dtype=PETSc.ScalarType)
lmbda.x.array[cells_1]  = np.full_like(cells_1, lmbda_1, dtype=PETSc.ScalarType)

The visualization produced by paraview is shown below.

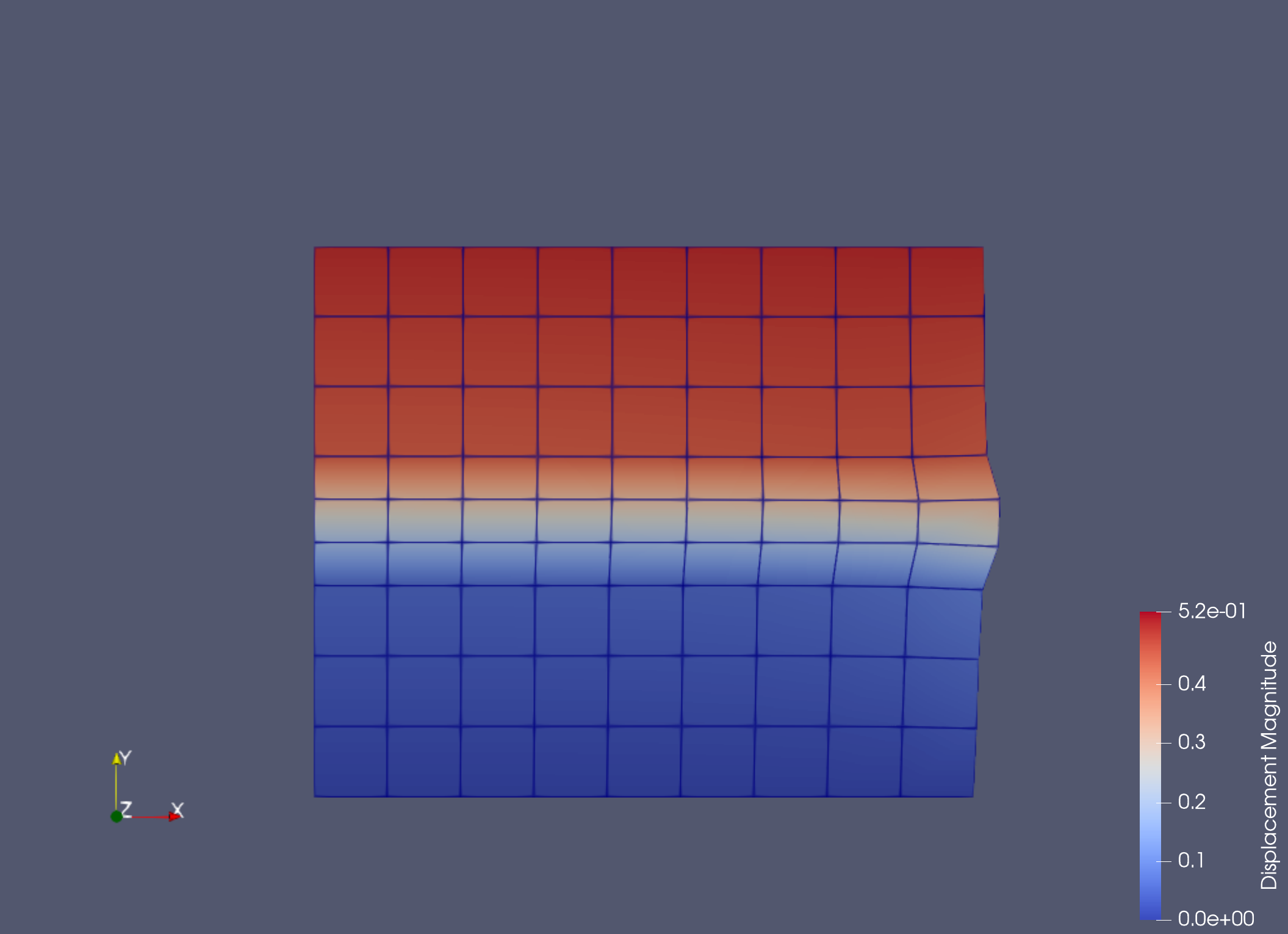
Deformed configuration, where the colors indicate the displacement in vertical direction.